Variables and Expressions
Objective Learn the notion of variable and
algebraic expression.
The most important concept in algebra is that of a variable.
This is a concept that you may have seen before, but it is
important to begin by reviewing and discussing this concept.
Remember that a variable is simply a letter or sometimes a symbol
used to represent a quantity. For example, suppose b represents
the number of boys in the class and g represents the number of
girls. A verbal expression like "There are 14 girls in the
class." can be written as an algebraic expression or
equation, which involves a variable.
g = 14
We can also write a verbal expression from an algebraic one.
Because we know that the variable b represents the number of boys
in the class, the algebraic equation b = 15 can be translated to
the verbal sentence "There are 15 boys in the class."
What is an algebraic expression?
Have a look at these definitions:
- A variable is a letter or symbol used to
represent a quantity.
- An algebraic expression consists of one
or more numbers and variables along with one or more
arithmetic operations.
Some examples of algebraic expressions are shown below.
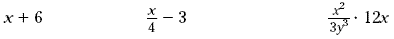
You might write a table like the following to show the
relation between verbal and algebraic expressions.
| Verbal Expression |
Algebraic Expression |
| 2 more than a number x |
x + 2 |
| The square of a number x divided by three
times a number y. |
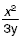 |
| The number of eyes in the
classroom (Let s represent the number of students in the
class.) |
2s + 2 or 2(s + 1) (Each student has
two eyes and the teacher has two eyes)
|
Remember the terms that describe expressions like x 5.
These expressions are called powers. The x is the base of the
power and the number 5 is called the exponent. The expression x
5 is described verbally as "x raised to the fifth
power" or simply "x to the fifth."
Translating between algebraic and verbal expressions.
Example 1
Write an algebraic expression for the sum of 3 and the number
x divided by 16.
Solution (3 + x ) ÷ 16 or 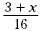 . .
Example 2
Write an algebraic expression for six subtracted from the
number y, all raised to the fourth power.
Solution ( y - 6) 4
Example 3
Write a verbal expression for 5m - n 2 .
Solution
The product of 5 and the number m minus the number n raised to
the second power (or n squared)
Example 4
Write a verbal expression for ( x + 2) y.
Solution
The sum of the number x and 2, all raised to the exponent y
(or the y th power)
There is one final term that you should describe to your
students in this lesson. To evaluate an
expression means to find its values. Use the following examples
to illustrate this definition.
Example 5
Evaluate 4 3 .
Solution
4 3 = 4 · 4 · 4 = 64
Example 6
Evaluate the expression ( x + 3) 2 when x = 3.
Solution
Substitute 3 for x in the expression. ( x + 3) 2 =
(3 + 3) 2 = 6 2 = 36
The processes of assigning variables to quantities and of
translating between verbal and algebraic expressions are
fundamental in algebra.
|