|
TUTORIALS:
|
Adding and Subtracting Fractions
Examples with solutions:
Example 1:
Perform the addition 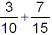 , and express your
final answer in simplest form.
solution:
The prime factorizations of the two denominators are
10 = 2 1 × 5 1
15 = 3 1 × 5 1
So, the prime factors 2, 3, and 5 occur, each to at most the
first power. Thus
LCD = 2 × 3 × 5 = 30
(Notice that this is smaller than the product, 10 × 15 = 150,
of the original denominators. The factor 5 occurs in both of the
original denominators, but need appear only once in the LCD.)
Now, to convert 3 / 10 to an equivalent fraction with a
denominator of 30, we need to multiply top and bottom by 30 / 10
= 3. To convert 7 / 15 to an equivalent fraction with denominator
of 30, we need to multiply top and bottom by 30 / 15 = 2. So
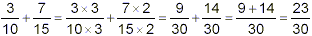
Since 23 is a prime number, no simplification of this result
is possible, and so our final answer is
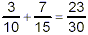
Example 2:
Perform the addition 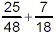 and express your final
answer in simplest form. {\b
solution:
First we write the two denominators as products of prime
factors:
48 = 2 4 × 3 1
18 = 2 1 × 3 2
Thus,
LCD = 2 x · 3 y
since the prime factorizations of 48 and 18 contain only 2 and
3 as factors.
| Then |
|
| |
x = 4, because the highest power of 2 is
4, occurring in the factorization of 48, |
| and |
|
| |
y = 2, because the highest power of 3 is
2, occurring in the factorization of 18. |
So,
LCD = 2 4 · 3 2 = 144.
Now, to convert 25 / 48 to an equivalent fraction with a
denominator of 144, we must multiply top and bottom by 144 / 48 =
3. To convert 7 / 18 to an equivalent fraction with a denominator
of 144, we must multiply top and bottom by 144 / 18 = 8. So, our
problem becomes
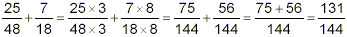
To check for the possibility of simplification, we need to
express the numerator and denominator of this result as a product
of prime factors. We already know that
144 = 2 4 · 3 2
It takes just a minute to verify that 131 is not divisible by
either 2, 3, 5, 7, or 11, and so 131 must be a prime number
already. Therefore no further simplification is possible and our
final answer is
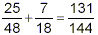
(In case you’re wondering why we had to check only that
none of 2, 3, 5, 7, and 11 divided evening into 131 to conclude
that 131 is a prime number – the reason is this. We
don’t have to check any divisors which are not prime numbers
themselves, or which are larger than the square root of the
number being factored. Since the square root of 131 is less than
12, we only have to check potential prime divisors which are less
than 12, and this is the list 2, 3, 5, 7, and 11.)
|
