|
TUTORIALS:
|
Systems of Equations That Have No Solution or Infinitely Many
Solutions
What happens when a system of equations has no solution or
infinitely many solutions?
This question is best addressed by examples.
Example 1
Solve the system of equations.
2x + 6y = 9
x + 3y = 4
Solution
Solve the second equation for x to get x = 4 - 3y. Then
substitute 4 - 3y for x in the first equation.
| 2x + 6y |
= 9 |
|
| 2(4- 3y ) + 6y |
= 9 |
Substitute 4 - 3y for x. |
| 8 - 6y + 6y |
= 9 |
Distributive Property |
| 8 |
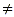 9 9 |
|
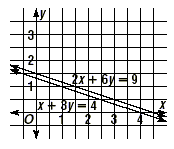
Since this equation is never true, there are no solutions to
the system. The graph of this system of equations is shown below.
Notice that the lines are parallel.
Key Idea
When solving a system of equations, if the final equation does
not contain a variable and is false, then there are no solutions.
Example 2
Solve the system of equations.
2x + 8y = 14
x + 4y = 7
Solution
Solve the second equation for x to get x = 7 - 4y. Then
substitute 7 - 4y for x in the first equation.
| 2x + 8y |
= 14 |
|
| 2(7 - 4y ) +8y |
= 14 |
Substitute 7 - 4y for x. |
| 14 - 8y + 8y |
= 14 |
|
| 14 |
= 14 |
|
This equation does not involve either variable, but the
equation is always true. In this case, there are infinitely many
solutions. The two lines are identical.
Key Idea
When solving a system of equations, if the final equation does
not contain a variable and is true, then there are infinitely
many solutions.
|