|
TUTORIALS:
|
Midpoint of a Line Segment
Objective Learn the algebraic formula for the
midpoint of a line segment, whose endpoints are given by ordered
pairs of numbers.
This is a relatively straightforward lesson, which shows that
the x- and y-coordinates of the midpoint of a line segment can be
obtained by taking the averages of the x- and y-coordinates,
respectively.
Begin by reembering the formula for the average of two numbers
x and y.
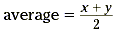
Take a look at the following diagram.
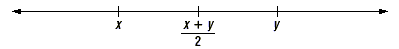
The average is the midpoint of the segment
between the two points, or the halfway point between x and y.
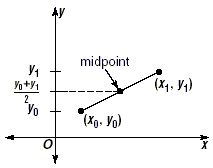
Two points in a plane have coordinates (x 0 , y
0) and (x 1 , y 1). How can we find
the coordinates of the midpoint of the segment joining them?
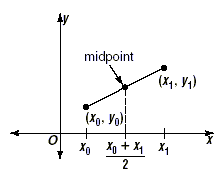
For two points in a plane, the halfway point between them
should have an x-coordinate that is halfway between the
x-coordinates of the two points. This is shown in the diagram
below.
In the same way, the y-coordinate of the midpoint is the
midpoint of the y-coordinates. The formula for the y-coordinate
of the midpoint is 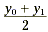 . This is shown in the diagram below.
The formula for the coordinates of the midpoint of a line
segment is given below.
Definition of Midpoint
The midpoint of the segment joining two points at (x 0
, y 0) and (x 1 , y 1) is given
by
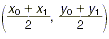
Now you should practice using the formula to find midpoints of
line segments.
Exercises
Find the coordinates of the midpoint of a segment with each
pair of endpoints.
1. A (9, 4), B (7, 6) (8, 5)
2. L (8, -2), M (0, 10) (4, 4)
3. X (2, 5), Y ( -6, 3) ( -2, 4)
4. T (1, -9), U (4, 7) (2.5, -1)
|
