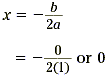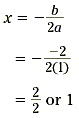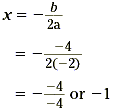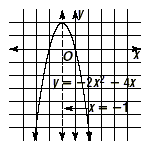Home |
Axis of Symmetry and Vertex of a ParabolaAxis of SymmetryParabolas are symmetric. Draw any parabola on a paper and fold it along a vertical line that goes right through the middle of the parabola. This line is called the axis of symmetry of the parabola. The two halves of the parabola match up after you folded along this line. Axis of Symmetry The equation of the axis of symmetry for the graph of the
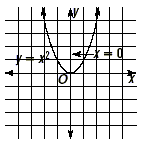
quadratic function y = ax 2 + bx + c , where a The reason why the axis of symmetry has this as its equation will be explained in a future lesson. Example 1 Find the equation of the axis of symmetry for the graph of y = x 2. Solution Write this function as y = 1x 2 + 0x + 0. So, a = 1, b = 0, and c = 0.
Therefore, the equation of the axis of symmetry is x = 0, which is the y-axis.
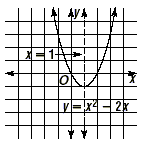
Example 2 Find the equation of the axis of symmetry for the graph of y = x 2 - 2x . Solution Write this function as y = x 2 - 2x + 0, so in this case a = 1, b = -2, and c = 0.
The equation of the axis of symmetry is x = 1.
Example 3 Find the equation of the axis of symmetry for the graph of y = -2x 2 - 4x . Solution Write this function as y = -2x 2 - 4x + 0 so that in this case a = -2, b = -4, and c = 0.
So the equation of the axis of symmetry is x = -1.
Vertex of a ParabolaThe axis of symmetry intersects the parabola at exactly one
point. This is called the vertex of the
parabola. This point is either the minimum point on the parabola
(as in Examples 1 and 2) or the maximum point (as in Example 3).
Graphically, the vertex is the tip of the parabola. If we know
the equation of the axis of symmetry
Example 6 Find the vertex of the graph of y = x 2 - 2x . Solution In Example 4, we found that the axis of symmetry of this parabola is x = 1. So the vertex has an x-coordinate equal to 1. To find the y-coordinate, substitute x = 1 into the equation. y = x 2 - 2x y = (1) 2 - 2(1) y = -1 So the y-coordinate of the vertex is -1. The vertex of this parabola is at (1, -1). This point is the minimum since, as the graph shows, the tip of the parabola is at the bottom.
Example 7 Find the vertex of the graph of y = - 2x 2 - 4 x . Solution In Example 5, we found that the axis of symmetry of this parabola is the line x = -1. So the vertex has an x -coordinate equal to -1. To find the y-coordinate, substitute x = -1 into the equation. y = -2x 2 - 4x y = -2(-1) 2 - 4(-1) y = 2 So 2 is the y-coordinate of the vertex. The vertex of this parabola is at ( -1, 2). This point is the maximum since, as the graph shows, the tip of this parabola is at the top. If you are given the coordinates of the vertex, how can you find the axis of symmetry of the parabola? Since the vertex lies on the axis of symmetry, which is vertical, the x-coordinate of the vertex will tell you the equation of the axis of symmetry. For example, if the vertex of a parabola is at the point (2, 3), then the axis of symmetry has equation x = 2. |
0, is 
. 
, then since the vertex
lies on the axis of symmetry, we know the x-coordinate of the
vertex 
. To find the
y-coordinate, substitute the x value into the equation of the
function.