|
TUTORIALS:
|
Standard Form of a Line
The graph of the equation x = 4 is a vertical line.
Because slope is undefined for vertical lines, the equation of this line cannot be
written in slope-intercept form or point-slope form. Only nonvertical lines can be
written in those forms. However, a vertical line can be written in standard form. For
example,
x = 4
can be written as
1 · x + 0
· y = 4.
Every line has an equation in standard form.
Example
Finding the equation of a line
Write an equation in standard form with integral coefficients for the line l through
(2, 5) that is perpendicular to the line 2x + 3y = 1.
Solution
First solve the equation 2x + 3y = 1 for y to find its slope:
| 2x + 3y |
= 1 |
|
| 3y |
= -2x + 1 |
|
| y |
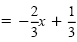 |
The slope is
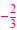 |
The slope of line l is the opposite of the reciprocal of
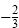 . So line l has slope . So line l has slope
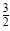 and
goes through (2, 5). Now use the point-slope form to write the equation: and
goes through (2, 5). Now use the point-slope form to write the equation:
| y - 5 |
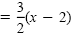 |
Point-slope form |
| y - 5 |
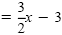 |
Distributive property |
| y |
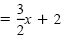 |
|
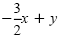 |
= 2 |
|
| 3x - 2y |
= -4 |
Multiply each side by -2. |
So 3x - 2y = -4 is the standard form of the equation of the line through (2, 5) that
is perpendicular to 2x + 3y = 1.
|