Home
Fields Medal Prize Winners (1998)

TUTORIALS:

Adding and Subtracting Monomials
Solving Quadratic Equations by Using the Quadratic Formula
Addition with Negative Numbers
Solving Linear Systems of Equations by Elimination
Rational Exponents
Solving Quadratic Inequalities
Systems of Equations That Have No Solution or Infinitely Many Solutions
Dividing Polynomials by Monomials and Binomials
Polar Representation of Complex Numbers
Solving Equations with Fractions
Quadratic Expressions Completing Squares
Graphing Linear Inequalities
Square Roots of Negative Complex Numbers
Simplifying Square Roots
The Equation of a Circle
Fractional Exponents
Finding the Least Common Denominator
Simplifying Square Roots That Contain Whole Numbers
Solving Quadratic Equations by Completing the Square
Graphing Exponential Functions
Decimals and Fractions
Adding and Subtracting Fractions
Adding and Subtracting Rational Expressions with Unlike Denominators
Quadratic Equations with Imaginary Solutions
Graphing Solutions of Inequalities
FOIL Multiplying Polynomials
Multiplying and Dividing Monomials
Order and Inequalities
Exponents and Polynomials
Fractions
Variables and Expressions
Multiplying by 14443
Dividing Rational Expressions
Division Property of Radicals
Equations of a Line - Point-Slope Form
Rationalizing the Denominator
Imaginary Solutions to Equations
Multiplying Polynomials
Multiplying Monomials
Adding Fractions
Rationalizing the Denominator
Rational Expressions
Ratios and Proportions
Rationalizing the Denominator
Like Radical Terms
Adding and Subtracting Rational Expressions With Different Denominators
Percents and Fractions
Reducing Fractions to Lowest Terms
Subtracting Mixed Numbers with Renaming
Simplifying Square Roots That Contain Variables
Factors and Prime Numbers
Rules for Integral Exponents
Multiplying Monomials
Graphing an Inverse Function
Factoring Quadratic Expressions
Solving Quadratic Inequalities
Factoring Polynomials
Multiplying Radicals
Simplifying Fractions 1
Graphing Compound Inequalities
Rationalizing the Denominator
Simplifying Products and Quotients Involving Square Roots
Standard Form of a Line
Multiplication by 572
Adding and Subtracting Fractions
Multiplying Polynomials
Factoring Trinomials
Solving Exponential Equations
Solving Equations with Fractions
Roots
Simplifying Complex Fractions
Multiplying and Dividing Fractions
Mathematical Terms
Solving Quadratic Equations by Factoring
Factoring General Polynomials
Adding Rational Expressions with the Same Denominator
The Trigonometric Functions
Solving Nonlinear Equations by Factoring
Solving Systems of Equations
Midpoint of a Line Segment
Complex Numbers
Graphing Systems of Equations
Reducing Rational Expressions
Powers
Rewriting Algebraic Fractions
Exponents
Rationalizing the Denominator
Adding, Subtracting and Multiplying Polynomials
Radical Notation
Solving Radical Equations
Positive Integral Divisors
Solving Rational Equations
Rational Exponents
Mathematical Terms
Rationalizing the Denominator
Subtracting Rational Expressions with the Same Denominator
Axis of Symmetry and Vertex of a Parabola
Simple Partial Fractions
Simplifying Radicals
Powers of Complex Numbers
Fields Medal Prize Winners (1998)

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

The Trigonometric Functions

There are two common approaches to the study of trigonometry. In one, the trigonometric functions are defined as ratios of two sides of a right triangle. In the other, these functions are defined in terms of a point on the terminal side of an angle in standard position. We define the six trigonometric functions, sine, cosine, tangent, cotangent, secant, and cosecant (abbreviated as sin, cos, etc.), from both viewpoints.

Definition of the Six Trigonometric Functions

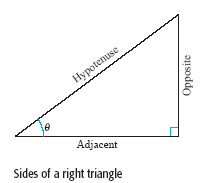
Right triangle definitions, where 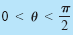(see the figure below)

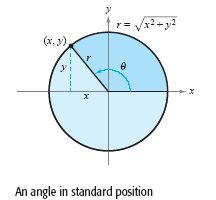
Circular function defiinitions, where θ is any angle (see the figure below).

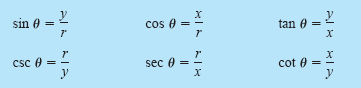
The following trigonometric identities are direct consequences of the definitions (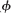 is the Greek letter phi).

Trigonometric Identities (Note that sin²θ is used to represent (sin θ)².)
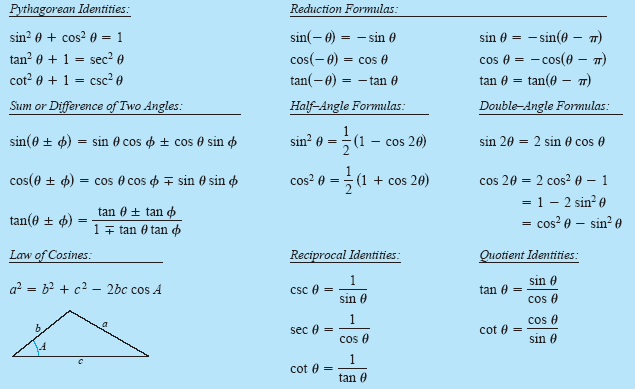