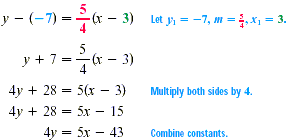|
Home |
Equations of a LineAn equation in two first-degree variables, such as has a line as its graph, so it is called a linear equation. In the rest of this section, we consider various forms of the equation of a line. 4 x + 7 y = 20, has a line as its graph, so it is called a linear equation. In the rest of this section, we consider various forms of the equation of a line. The slope-intercept form of the equation of a line involves the slope and the y-intercept. Sometimes, however, the slope of a line is known, together with one point (perhaps not the y-intercept) that the line goes through. The point-slope form of the equation of a line is used to find the equation in this case. Let (x1, y1) be any fixed point on the line and let (x, y) represent any other point on the line. If m is the slope of the line, then by the definition of slope,
or y - y1 = m(x - x1)
Point-slope form If a line has slope m and passes through the point (x1, y1), then an equation of the line is given by y - y1 = m(x - x1) the point-slope form of the equation of a line.
Example Point-Slope Form Find an equation of the line that passes through the point (3, -7) and has slope m = 5/4. Solution Use the point-slope form.
The equation of the same line can be given in many forms. To avoid confusion, the linear equations used in the rest of this section will be written in slopeintercept form, y = mx + b, which is often the most useful form. The point-slope form also can be useful to find an equation of a line if we know two different points that the line goes through. The procedure for doing this is shown in the next example. Example Using Point-Slope Form to Find Equation Find an equation of the line through (5, 4) and (-10, -2). Solution Begin by using the definition of slope to find the slope of the line that passes through the given points.
Either (5, 4) or (-10, -2) can be used in the point-slope form with m = 2/5. If (x1, y1) = (5, 4) then y - y1 = m(x - x1)
Check that the same result is found if (x1, y1) = (-10, -2). Example Horizontal Line Find an equation of the line through (8, -4) and (-2, -4). Solution Find the slope.
Choose, say, (8, -4) as (x1, y1).
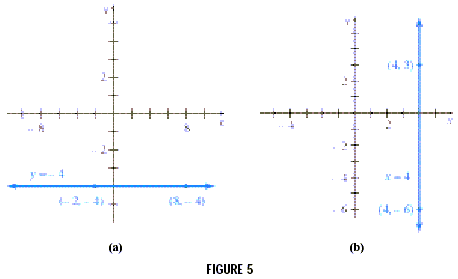
Plotting the given ordered pairs and drawing a line through the points, show that the equation y = -4 represents a horizontal line. See Figure 5(a). Every horizontal line has a slope of zero and an equation of the form y = k where k is the y-value of all ordered pairs on the line.
Example Vertical Line Find an equation of the line through (4, 3) and (4, -6). Solution The slope of the line is
which is undefined. Since both ordered pairs have x-coordinate 4, the equation is x = 4. Because the slope is undefined, the equation of this line cannot be written in the slope-intercept form. Again, plotting the given ordered pairs and drawing a line through them show that the graph of x = 4 is a vertical line. See Figure 5(b). The slope of a horizontal line is 0. The slope of a vertical line is undefined.
|
||||||||