|
TUTORIALS:
|
Complex Numbers
Euler’s formula
A useful expression is Euler’s formula which expresses an exponential with imaginary argument in terms of a sum of real and imaginary parts:
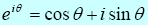
We can see where this comes from using the series representations of the exponential, sine and cosine functions
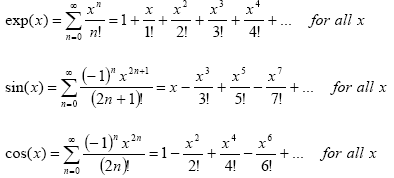
If we extend the exponential series expression for imaginary argument z = iθ where θ is real, then
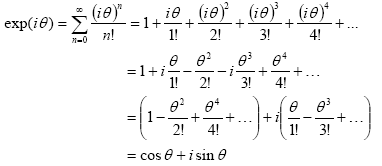
Exponential form: Using Euler’s formula, it is possible to compactly write a complex number in terms of an exponential function:
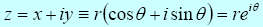
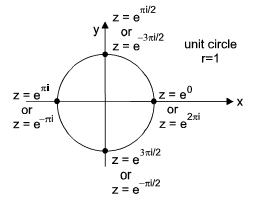
On an Argand diagram, complex numbers with the same modulus r =
| z | but different arguments θ make up points on a circle centred on the origin with radius
r = | z |. For modulus r = 1, the circle is of radius equal to one. Special points of interest (for
r = 1) are:
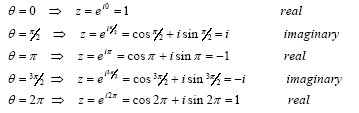
|