Solving Rational Equations
Equations whith Fractions
When an equation includes fractions, first eliminate all
denominators by multiplying both sides of the equation by a
common denominator, a number that can be divided (with no
remainder) by each denominator in the equation. When an equation
involves fractions with variable denominators, it is necessary to
check all solutions in the original equation to be sure that no
solution will lead to a zero denominator.
EXAMPLE
Solve each equation.
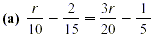
Solution
The denominators are 10, 15, 20, and 5. Each of these numbers
can be divided into 60, so 60 is a common denominator. Multiply
both sides of the equation by 60 and use the distributive
property. (If a common denominator cannot be found easily, all
the denominators in the problem can be multiplied together to
produce one.
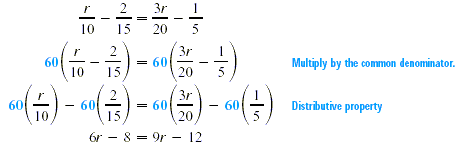
Add -9r and 8 to both sides.
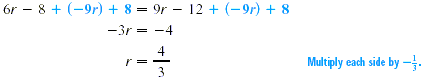
Check by substituting into the original equation.
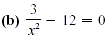
Solution
Begin by multiplying both sides of the equation by x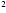 to get 3 - 12x to get 3 - 12x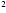 = 0. This equation could be solved by using the
quadratic formula with a = -12, b = 0 and c = 3. Another method,
which works well for the type of quadratic equation in which b =
0 is shown below. = 0. This equation could be solved by using the
quadratic formula with a = -12, b = 0 and c = 3. Another method,
which works well for the type of quadratic equation in which b =
0 is shown below.
3 - 12x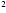 = 0 = 0
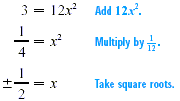
Verify that there are two solutions, -1/2 and 1/2.
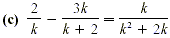
Solution
Factor k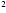 + 2k as k(k + 2). The least common
denominator for all the fractions is k(k + 2). Multiplying both
sides by k(k + 2) gives the following. + 2k as k(k + 2). The least common
denominator for all the fractions is k(k + 2). Multiplying both
sides by k(k + 2) gives the following.
2(k + 2) - 3k(k) = k
2k + 4 -3k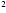 = k Distributive property = k Distributive property
-3k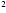 - k + 4 = 0 Add -k; rearrange terms - k + 4 = 0 Add -k; rearrange terms
3k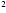 + k - 4 = 0 Multiply by -1 + k - 4 = 0 Multiply by -1
(3k - 4)(k + 1) = 0 Factor
3k - 4 = 0 or k + 1 = 0
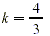 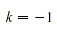
Verify that the solutions are 4/3 and -1.
CAUTION
It is possible to get, as a solution of a rational equation, a
number that makes one or more of the denominators in the original
equation equal to zero. That number is not a solution, so it is
necessary to check all potential solutions of rational equations.
These introduced solutions are called extraneous solutions.
EXAMPLE
Solve
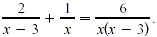
Solution
The common denominator is x(x-3). Multiply both sides by
x(x-3) and solve the resulting equation.
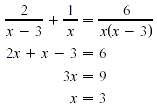
Checking this potential solution by substitution in the
original equation shows that 3 makes two denominators 0. Thus 3
cannot be a solution, so there is no solution for this equation.
|