|
TUTORIALS:
|
Simplifying Fractions
An indispensable aspect of any work with algebraic fractions
is simplification of the result. We will demonstrate techniques
for simplification of fractions throughout these notes where the
need arises, but in this specific document, we’ll set the
stage by working through a number of examples, focussing
primarily on the strategies for simplification themselves.
Despite the differences in appearance of the examples to follow,
there really is just one approach available for simplifying
fractions:
(i) factor the numerator and denominator as completely as
possible, and then
(ii) cancel any factors the numerator and denominator have in
common.
If you take care to always do step (i) as a separate explicit
step of work, you will rarely go wrong in simplifying fractions.
What follows in this document is a series of quite a few worked
out examples. They tend to be quite repetitive because there is
just the one simple strategy just described, which must be
applied to each one. Don’t just read through the rest of
this document quickly to notice how easily we’ve worked out
the solutions (and perhaps to notice how boring this sort of
stuff can become). Instead, after studying the first few examples
carefully, use the remaining examples as practice problems: cover
up the solutions and try to work them out on your own. When you
are done in each case, compare your method and final result with
the one we’ve given.
Example 1:
Simplify 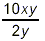 . .
solution:
The numerator and denominator of this fraction are already
nearly fully factored. Using brackets to make these factors
explicit, we get
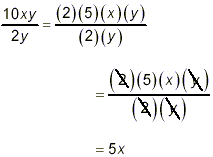
as the final result.
Example 2:
Simplify 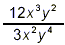 . .
solution:
Writing the numerator and denominator with the factors
explicitly separated gives
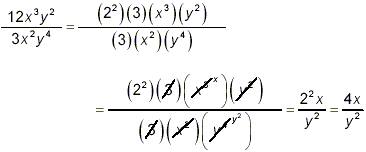
Example 3:
Simplify 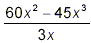 . .
solution:
The denominator is factored, but the numerator is not
factored. Using the stepwise approach for factoring illustrated
earlier in these notes, we get
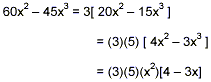
Thus
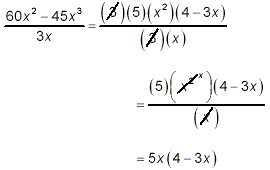
as the final result. There is no need to multiply this last
form out to remove the brackets, unless there had been some
specific instruction to do so.
Note that the first step of factoring is absolutely essential
here in order to get a correct result – a simpler
mathematical expression which is mathematically equivalent to the
original expression. A common error is to just focus on one of
the terms in the numerator:
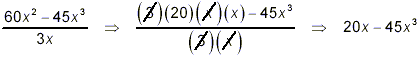
This “simplified” expression is not equivalent to
the original fraction, and so an error has been made. You can
easily demonstrate this by doing a test calculation:
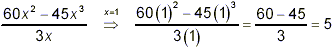
but
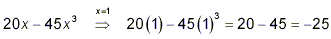
ince for this one value of x, the expression 20x – 45x
3 does not give the same value that the original fraction
gives, we know that 20x – 45x 3 cannot be a
correct simplification of the original fraction. The error came
from the fact that we cancelled the 3x of the denominator into
just one of the terms in the numerator. Instead, a valid
cancellation must be against factors of the entire numerator, as
was done in the original solution of this example.
|