Solving Nonlinear Equations by Factoring
A linear equation in one variable is an equation that can be written in the
form
ax + b = 0 where a and b are real numbers and a ≠ 0.
For example, the following are linear equations:
| 3x + 2(x - 5) = -2 |
2y - 3 = 5 + 3y |
 |
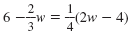A nonlinear equation is an equation that cannot be written in the form
ax + b = 0.
For example, the following are nonlinear equations:
| x2 + 5x + 6 = 0 |
 |
 |
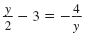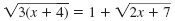Note:
Recall that a linear function is a
function that can be written as
f(x) = ax + b or y = ax + b, where a ≠ 0.
The equation 3x + 2(x - 5) = -2
be rewritten as 5x - 8 = 0, which is in the linear form
ax + b = 0.
Some nonlinear equations can be solved by factoring.
Procedure —
To Solve a Nonlinear Equation by Factoring
Step 1 Write the equation in standard form.
Step 2 Factor.
Step 3 Use the Zero Product Property.
Step 4 Solve for the variable.
Note:
A polynomial is in standard form when the
terms are arranged in descending order by
degree on the left side of the equation and
the right side of the equation is 0.
For example,
4x3 - 8x2 - 5x + 10 = 0 is in standard form.
Zero Product Property:
If P · Q = 0 then P = 0 or Q = 0. Or, P = 0 and Q
= 0.
Example 1
Solve for x:
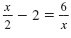
| Solution
|
 |
 |
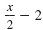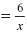| Step 1 Write the equation in standard form.
|
 |
 |
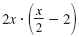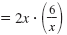| Multiply each side by the LCD, 2x.
Simplify.
Subtract 12 from both sides.
Step 2 Factor. Step 3 Use the Zero Product Property.
Step 4 Solve for the variable. |
x2 - 4x x2 - 4x - 12
(x - 6)(x + 2)
x - 6 = 0 or
x = 6 or
x2 - 4x - 12 |
= 12 = 0
= 0
x + 2 = 0
x = -2
= 0 |
The equation
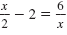 has the same solutions as x2 - 4x - 12
= 0.
Thus, the solutions are x = 6 and x = -2.
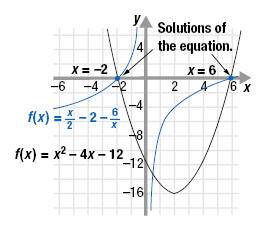
The graph of the corresponding functions,
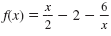 and
f(x) = x2 - 4x - 12 are shown. Even though the graphs are different they
both cross the x-axis at x = -2 and x = 6, the solutions of the equations.
Note:
To factor x2 - 4x - 12, find two integers
whose product is -12 and whose sum is -4. They are -6 and 2.
|
