|
TUTORIALS:
|
Simplifying Square Roots
by Removing Perfect Square Factors
We can exploit the rules for multiplication of square roots to
attempt to rewrite square roots in what is considered to be a
simpler form. Here,
“simpler square roots” means “the number inside
the square root is smaller”
“Simplifying a square root” means rewriting it as an
expression of the same value, but with the number or expression
inside the square root as small or simple as possible.
We will illustrate the technique here for square roots
involving just numbers, but this method is most important in
simplifying square roots containing algebraic expressions.
As an example, notice that we can do the following:
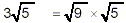 |
|
because 3 and 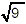 represent the
same number represent the
same number |
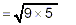 |
|
by the rule for multiplying square roots
together |
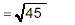 |
|
|
Thus 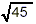 has the same value as has the same value as 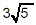 . But, we would consider . But, we would consider 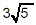 to be a simpler form because the quantity
in the square root is a smaller number. If we rewrite the above
example with the steps in reverse order, we can see the strategy
for simplifying a square root when that is possible. to be a simpler form because the quantity
in the square root is a smaller number. If we rewrite the above
example with the steps in reverse order, we can see the strategy
for simplifying a square root when that is possible.
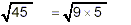 |
|
If possible, separate or factor 45 into a
product of two numbers, one of which is the square of a
whole number. (Recall, we called such numbers
“perfect squares” earlier.) |
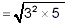 |
|
|
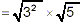 |
|
Use the rule for multiplying two square
roots. |
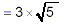 |
|
since the square root of a square is the
original number. |
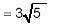 |
|
The multiplication symbol can be omitted.
|
Since the remaining number in the square root, the 5,
obviously cannot be written as a product of a perfect square and
another number, we have achieved as much simplification here as
is possible.
This strategy for simplifying square root expressions requires
us to develop a strategy for deducing how numbers can be
rewritten as a product involving one or more perfect squares
– indeed, we need to be able to rewrite the original number
in the square root as a product of perfect squares, and the one
smallest value which is not a perfect square.
|