Solving Systems of Equations - Two Lines
Intersecting lines should be solved algebraically, even if the directions say to solve graphically.
⇒ Recall: Two algebraic methods for solving systems of equations are addition and
substitution.
Example 1:
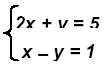
Check:
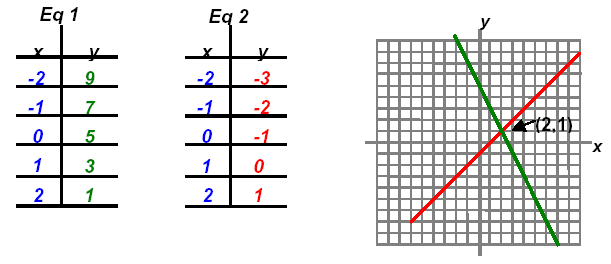
adding these equations gives 3x = 6 which yields x = 2.
Substituting in equation 2: (2) - y = 1 which yields y = 1.
The solution is the point (2,1) or S = { (2,1) }.
Example 2:
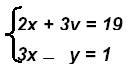
Check:
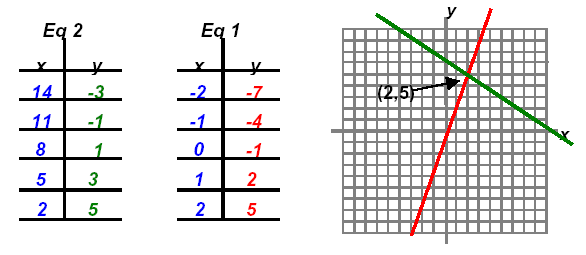
Multiple the second equation by 3 and obtain:
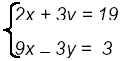
Adding these equations gives 11x = 22 or x = 2.
Substitute in second equation: 3(2) - y = 1 or y = 5.
Check by substituting both in first equation: 2(2) + 3(5) = 19
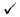
Thus, the solution is the point (2,5) or S = { (2,5) }.
Example 3:
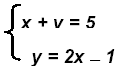
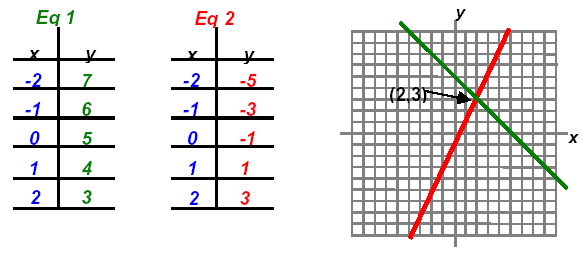
The solution is the point (2, 3) or { (2, 3) }
Since the second equation is already solved for y use the expression as a replacement for y in the
first equation:
x + (2x − 1) = 5 which gives us an equation in x alone.
3x = 6 or x = 2. Substitute in the second equation to solve for y.
y = 2(2) − 1 or y = 3. To check substitute both in the first equation: 4 + 7
= 5

Example 4:
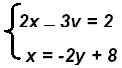
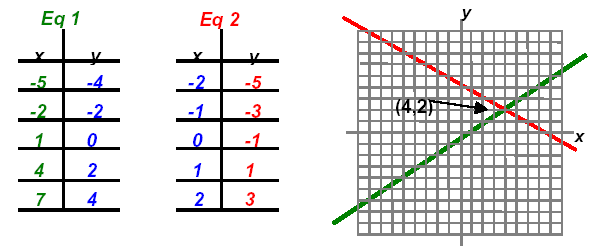
The solution is the point (4, 2) or { (4, 2) }
Since the second equation is already solved for y use the expression as a replacement for y in the
first equation:
2·(-2y + 8) − 3y = 2 which gives us an equation in y alone.
- 7y = -14 or y = 2. Substitute in the second equation to solve for x.
x = -2(2) + 8 or x = 4. To check substitute both in the first equation: 8 − 6
= 2

|