Polar Representation of Complex Numbers
The Argand diagram
In two dimensional Cartesian coordinates (x,y), we are used to plotting the function
y(x) with y on the vertical axis and x on the horizontal axis.
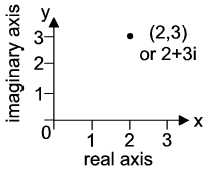
In an Argand diagram, the complex number z = x + iy is plotted as a single point with coordinates (x,y). The horizontal axis is called the real axis (x-axis) and the vertical axis is called the imaginary axis (y-axis).
As in usual Cartesian coordinates, the distance from the origin to a point
(x, y) is equal to
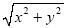 . This is equal to the modulus
| z | of the complex number
z = x + iy.
The Argand diagram may also be called the complex plane. It stresses that complex numbers are a generalisation of real numbers, that lie on the horizontal axis only.
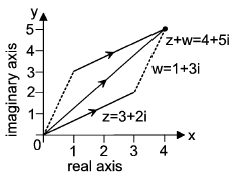
The expression z = x + iy is known as the Cartesian form or the rectangular form of the complex number z. Using the Argand diagram, we can see that the addition of complex numbers behaves like the addition of vectors.
If we express z = x + iy as an ordered pair (x, y), then the addition of two complex numbers may be defined by
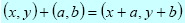
in the same way as the addition of two vectors.
Polar coordinates
A position vector of a point in two dimensions may be expressed in terms of Cartesian coordinates (x,y) and plotted with y on the vertical axis and x on the horizontal axis.
It is also possible to express the two dimensional position vector in terms of polar coordinates (r,θ) where r is the magnitude of the vector (distance from origin to the point) and θ is the angle between the position vector and the positive x-axis.
The Cartesian and polar coordinates are related by:
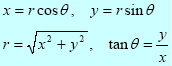
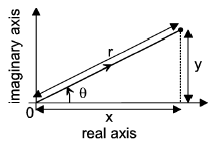
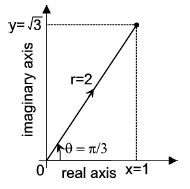
In the same way, the complex number z = x + iy may be expressed in polar coordinates (r,
θ), in its polar form:
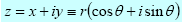
where
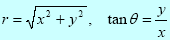
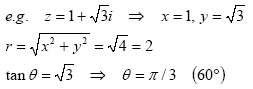
The modulus of a complex number
In polar coordinates (r, θ) the magnitude r of the distance from the origin to the point represented by
z is equal to the modulus of the complex number |
z |:
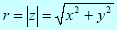
The argument of a complex number
In polar coordinates (r, θ) the angle θ is known as the argument of the complex number
z, denoted θ = arg(z).
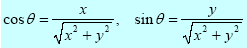
There is a complication because a single point on the Argand diagram does not correspond to a single complex number. The reason is that we can add
2π to the value of the argument θ in order to produce a different complex number, but when plotted on the Argand diagram, the two numbers are plotted in the same place.
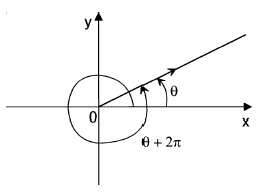
Principal value: If we want to uniquely define the value of the argument θ we can impose the condition
−π<θ≤π so that θ is known as the principal value of the argument.
For the complex number z = x + iy, the argument θ is given by the solution of the equations:
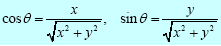
or
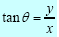
If the second expression tan θ = y/x is used to determine θ, it is wise to plot
z = x + iy on an Argand diagram to check that the answer is correct.
|
