|
TUTORIALS:
|
Graphing Systems of Equations
A set of equations with the same variables forms a system of
equations . A solution to a system of two equations with two
variables is an ordered pair of numbers that satisfies both
equations. One way to solve a system of equations is to carefully
graph the equations on the same coordinate plane. The coordinates
of the point at which the graphs intersect is the solution to the
system. If the graphs of the two equations coincide, meaning they
are the same line, then there are infinitely many solutions to
the system. A system of equations with at least one ordered pair
that satisfies both equations is consistent. It is possible for
the graphs of the two equations to be parallel. In this case, the
system is inconsistent because there are no solutions that
satisfy the two equations.
Example
Graph the system of equations to find the solution.
y = 2x - 3 and y = x - 1
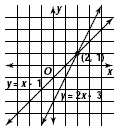
The graphs appear to intersect at the point with coordinates
(2, 1).
Check this estimate by replacing x with 2 and y with 1 in each
equation.
Check:
| y = 2x - 3 |
y = x - 1 |
| 1 = 2(2) - 3 |
1 = 2 - 1 |
| 1 = 1 |
1 = 1 |
The solution is (2, 1).
|