|
TUTORIALS:
|
Graphing Compound Inequalities
Graphing the Solution Set to a Compound Inequality
The following example shows a compound inequality that has no solution and one
that is satisfied by every real number.
Example 1
All or nothing
Sketch the graph and write the solution set in interval notation to each compound
inequality.
a) x < 2 and x > 6
b) x < 3 or x > 1
Solution
a) A number satisfies x < 2 and x > 6 if it is both less than 2 and greater than 6.
There are no such numbers. The solution set is the empty set,
Ø.
b) To graph x < 3 or x > 1, we shade both regions on the same number line as
shown in the figure below. Since the two regions cover the entire line, the solution set
is the set of all real numbers (-∞,
∞).
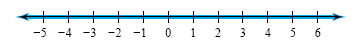
If we start with a more complicated compound inequality, we first simplify each
part of the compound inequality and then find the union or intersection.
Example 2
Intersection
Solve x + 2 > 3 and x - 6 < 7. Graph the solution set.
Solution
First simplify each simple inequality:
| x + 2 - 2 |
> 3 - 2 |
and |
x - 6 + 6 |
< 7 + 6
|
| x |
> 1 |
and |
x |
< 13 |
The intersection of these two solution sets is the set of numbers between (but not
including) 1 and 13. Its graph is shown in the figure below. The solution set is written in
interval notation as (1, 13).
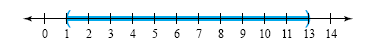
Example 3
Union
Graph the solution set to the inequality
5 - 7x ≥ 12 or 3x - 2 < 7.
Solution
First solve each of the simple inequalities:
| 5 - 7x - 5 |
≥ 12 - 5 |
or |
3x - 2 + 2 |
< 7 + 2
|
| -7x |
≥ 7 |
or |
3x |
< 9 |
| x |
≥ -1 |
or |
x |
< 3 |
The union of the two solution intervals is (-∞, 3). The graph is shown in
the figure below.
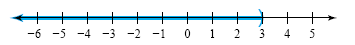
|