|
TUTORIALS:
|
Subtracting Mixed Numbers with Renaming (Borrowing)
Recall from our discussion of subtracting whole numbers that,
in problems in which a digit in the subtrahend is larger than the
corresponding digit in the minuend, we need to borrow.
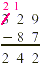
A similar situation can arise when we are subtracting mixed
numbers. If the fraction on the bottom is larger than the one on
top, we rename (or borrow from) the whole number on top.
To Add (or Subtract) Mixed Numbers with Different
Denominators
- rewrite the fractions as equivalent fractions with a
common denominator, usually the LCD;
- when subtracting, rename (or borrow from) the whole
number on top if the fraction on the bottom is larger
than the fraction on top;
- add (or subtract) the numerators, keeping the same
denominator;
- add (or subtract) the whole numbers; and
- write the answer in simplest form.
EXAMPLE 1
Subtract: 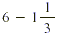 . .
Solution
Let’s rewrite the problem vertically.
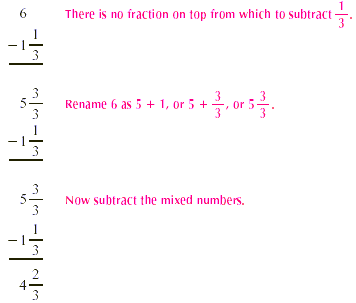
So 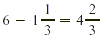
As in any subtraction problem, we can check our answer by
addition.
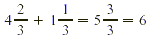
TIP
Recall that 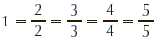 and so on. That is, any fraction having
the same numerator and denominator (both nonzero) equals 1. and so on. That is, any fraction having
the same numerator and denominator (both nonzero) equals 1.
EXAMPLE 2
Compute: 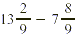
Solution
First, we write the problem vertically.
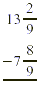
Because 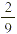 is larger than is larger than 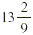 we need to rename we need to rename 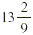 . .
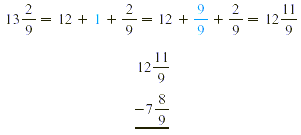
Finally, we subtract and then write the answer in simplest
form.
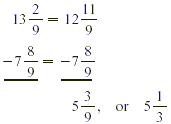
EXAMPLE 3
Find the difference between 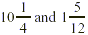 . .
Solution
First, we write the equivalent fractions, using the LCD.
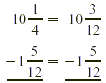
Then, we subtract by renaming.
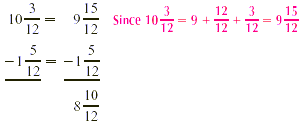
Simplifying the answer, we get 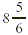 . .
EXAMPLE 4
You hike from point A to point B along a trail. If the entire
trail is 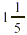 miles long, will you have more or less
than miles long, will you have more or less
than 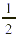 mile left to hike when you get to point
B? mile left to hike when you get to point
B?
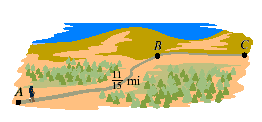
Solution
First we must find the difference between the length of the
entire trail, 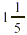 miles, and the distance hiked, miles, and the distance hiked, 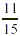 mile. mile.
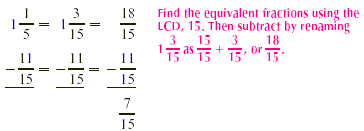
The distance left to hike is 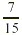 mile. Finally, we compare mile. Finally, we compare 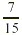 mile and mile and 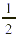 mile. mile.

Because 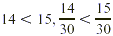 . Therefore . Therefore 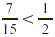 and you have less than and you have less than 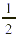 mile left to hike when you get to point
B. mile left to hike when you get to point
B.
|