|
TUTORIALS:
|
Multiplying Monomials
Objective Learn what polynomials by knowing
how to use the laws of exponents to multiply monomials.
To this point, you surely have worked with linear expressions
and equations. Now you need to understand how to do algebra with
higher degree expressions, involving higher powers of the
variables. The key ideas in this lesson are the laws of
exponents, which are used to simplify monomial expressions.
Monomials
Let's begin by reviewing exponents. If x is a
variable, then x 2 denotes x · x , x 3
denotes x · x · x , and more generally, x n denotes
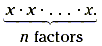
Definition of Monomials
A monomial is a number, a variable, or a
product of numbers and variables.
• Numbers are referred to as constants.
• When there are several occurrences of the same
variable, the expression is typically written in exponent form.
Monomials: 5x 2 , 7 xy , -3x 3 , 4y , z
100
Not Monomials: 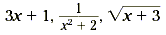
Laws of Exponents and Multiplying Monomials
When multiplying monomials, analyze the product of two powers
of the same variable, for instance, x 2 · x 3
. A good way to illustrate this is by multiplying various powers
of 2 together.
Example 1
Simplify 2 2 · 2 3.
Solution
2 2 · 2 3 = 4 · 8 = 32 = 2 5
2
Example 2
Simplify 2 4 · 2 5 .
Solution
2 4 · 2 5 = 16 · 32 = 512 = 2 9
In Examples 1 and 2, the exponent of the result of the
multiplication is the sum of the exponents in the two factors. In
Example 1, 5 = 2 + 3, and in Example 2, 9 = 4 + 5. Why is this
true? Recall that exponents are just shorthand for a repeated
product of the same number or variable. So,
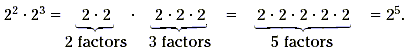
In general, when multiplying x m and x n , the result is as
follows.
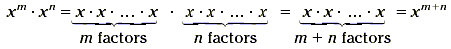
Product of Powers
When a power of x is multiplied by another power of x, the
result is a power of x whose exponent is the sum of the exponents
of the factors.
x m · x n = x m + n
This is true for any number or variable x , and for any whole
numbers m and n . Now use this idea to multiply monomials.
Example 3
Simplify 3x 5 · 4x 2 .
Solution
| 3x 5 · 4x
2 |
= (3 · 4) · ( x 5 · x
2 ) |
| |
= 12 x 5 + 2 or 12x 7
|
Notice that the constants are grouped together and the
variables are grouped together.
Example 4
Simplif 9y 8 · ( - y 7 ).
Solution
9y 8 · ( - y 7 ) = [9 · ( -1)] · ( y
8 · y 7 ) = -9y 15
|