Rationalizing the Denominator
A. What It Means to Rationalize the Denominator
In order that all of us doing math can compare answers, we
agree upon a common conversation, or set of rules, concerning the
form of the answers.
For instance, we could easily agree that we would not leave an
answer in the form of 3 + 4, but would write 7 instead.
When the topic switches to that of radicals, those doing math
have agreed that a RADICAL IN SIMPLE FORM will not (among other
things) have a radical in the denominator of a fraction. We will
all change the form so there is no radical in the denominator.
Now a radical in the denominator will not be something as
simple as 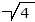 . Instead, it will have a radicand which
will not come out from under the radical sign like  .
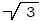Since 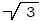is an irrational number, and we need to
make it NOT irrational, the process of changing its form so it is
no longer irrational is called RATIONALIZING THE DENOMINATOR.
B. There are 3 Cases of Rationalizing the Denominator
1. Case I : There is ONE TERM in the
denominator and it is a SQUARE ROOT.
2. Case II : There is ONE TERM in the
denominator, however, THE INDEX IS GREATER THAN TWO. It might be
a cube root or a fourth root.
3. Case III : There are TWO TERMS in the
denominator.
Let's study Case II:
2. Case II : There is ONE TERM in the
denominator, however, THE INDEX IS GREATER THAN TWO. It might be
a cube root or a fourth root.
Example:
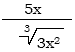 For the first part of this discussion, we
will ignore the top and\par concentrate on the denominator.
Procedure: Multiply top and bottom by
whatever works in order to create a perfect cube in the
denominator.
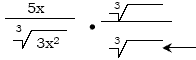 We need to multiply the bottom by
something that will make the result a cube...
 So we can take the cube root of it here...
 Which would cause the radical to be gone
down here.
Well...
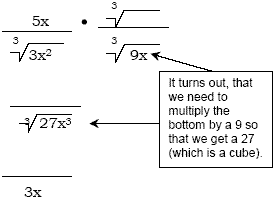
But we also need to multiply it by an x so that we get x
3 (which is also a cube).
So there, we've gotten rid of the radical in the denominator.
We've, therefore, rationalized the denominator. Now we'll look at
the entire problem with the numerator included this time.
Remember, whatever we do to the bottom, we must also do to the
top.
Original problem:
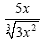
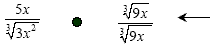 Here is our adjustment --- what we
needed to multiply top and bottom by so the bottom would become a
perfect square.
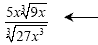 And here we see the result of our
multiplication on the bottom. We've created something of which we
can take the cube root.
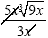 Notice we can cancel the Xs since they
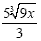are factors and represent the same number.
 Answer
|
