|
TUTORIALS:
|
Factors and Prime Numbers
What Factors Mean and Why They Are Important
Recall that in a multiplication problem, the whole numbers
that we are multiplying are called factors. For
instance, 2 is said to be a factor of 8 because 2 · 4 = 8.
Likewise, 4 is a factor of 8.
Another way of expressing the same idea is in terms of
division: We say that 8 is divisible by 2, meaning that there is
a remainder 0 when we divide 8 by 2.
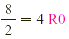
Note that 1, 2, 4, and 8 are all factors of 8.
Although we factor whole numbers, a major application of
factoring involves working with fractions, as we demonstrate in
the next section.
Finding Factors
To identify the factors of a whole number, we divide the whole
number by the numbers 1, 2,3, 4, 5, 6, and so on, looking for
remainders of 0.
EXAMPLE 1
Find all the factors of 6.
Solution
Starting with 1, we divide each whole number into 6.
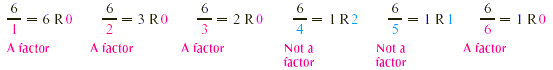
So the factors of 6 are 1, 2, 3, and 6. Note that
- 1 is a factor of 6 and that
- 6 is a factor of 6.
- We did not need to divide 6 by the numbers 7 or greater.
The reason is that no numberlarger than 6 could divide
evenly into 6, that is, divide into 6 with no remainder.
TIP
For any whole number, both the number itself and 1 are always
factors. Therefore all whole numbers (except 1) have at least two
factors.
When checking to see if one number is a factor of another, it
is generally faster to use the following divisibility
tests than to divide.
| The number is
divisible by |
if
|
| 2 |
the ones digit is 0, 2, 4, 6, or 8, that
is, if the number is even. |
| 3 |
the sum of the digits is divisible by 3. |
| 4 |
the number named by the last two digits
is divisible by 4. |
| 5 |
the ones digit is either 0 or 5. |
| 6 |
the number is even and the sum of the
digits is divisible by 3. |
| 9 |
the sum of the digits is divisible by 9. |
| 10 |
the ones digit is 0. |
Note that divisibility by 6 is equivalent to divisibility by
both 2 and 3.
|