|
TUTORIALS:
|
Finding the Least Common Denominator
To add fractions with denominators that are not identical, we use the basic principle
of rational numbers to build up the denominators to the least common denominator
(LCD). For example,
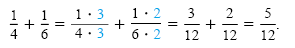
The LCD 12 is the least common multiple (LCM) of the numbers 4 and 6.
Finding the LCM for a pair of large numbers such as 24 and 126 will help you
to understand the procedure for finding the LCM for any polynomials. First factor
the numbers completely:
| 24 |
= 23 · 3 |
| 126 |
= 2 · 32 · 7 |
Any number that is a multiple of both 24 and 126 must have all of the factors of 24
and all of the factors of 126 in its factored form. So in the LCM we use the factors
2, 3, and 7, and for each factor we use the highest power that appears on that
factor. The highest power of 2 is 3, the highest power of 3 is 2, and the highest
power of 7 is 1. So the LCM is 23 · 32 · 7. If we write this product without
exponents, we can see clearly that it is a multiple of both 24 and 126:
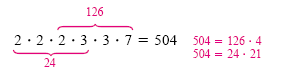
The strategy for finding the LCM for a group of polynomials can be stated as
follows.
Strategy for Finding the LCM for Polynomials
1. Factor each polynomial completely. Use exponents to express repeated
factors.
2. Write the product of all of the different factors that appear in the
polynomials.
3. For each factor, use the highest power of that factor in any of the
polynomials.
Helpful hint
The product of 24 and 126 is
3024 and 3024 is a common
multiple but not the least
common multiple of 24 and
126. If you divide 3024 by 6,
the greatest common factor
of 24 and 126, you get 504.
Example 1
Finding the LCM
Find the least common multiple for each group of polynomials.
a) 4x2y, 6y
b) a2bc, ab3c2, a3bc
c) x2 + 5x + 6, x2 + 6x + 9
Solution
a) Factor 4x2y and 6y as follows:
4x2y = 22 · x2y, 6y = 2 · 3y
To get the LCM, we use 2, 3, x, and y the maximum number of times that each
appears in either of the expressions. The LCM is 22 · 3 · x2y, or 12x2y.
b) The expressions a2bc, ab3c2, and a3bc are already factored. To get the LCM, we
use a, b, and c the maximum number of times that each appears in any of the
expressions. The LCM is a3b3c2.
c) Factor x2 + 5x + 6 and x2 + 6x + 9 completely:
x2 + 5x + 6 = (x + 2)(x + 3), x2 + 6x + 9 = (x + 3)2
The LCM is (x + 2)(x + 3)2.
|