Solving Exponential Equations
Determine the Value of X that makes the equation true (or
satisfies the equation)
8 x - 2 = 2 x + 4
Solution 1  guess and check guess and check
Sub in different values of x, trying to get closer and closer.
| X |
LS |
RS |
LS = RS |
| 1 |
1/8 |
32 |
NO |
| 2 |
1 |
64 |
NO |
| 5 |
512 |
512 |
YES |
Not a very efficient way of solving equations.
Solution 2  equating the bases equating the bases
If an equation can be re-arranged so that the bases are the
same, this means the exponents than have to be equivalent as a
result.
In this case we can re-write 8 with a base of 2 and an
exponent of 3. Using exponent laws we see that:
| 8 x - 2 |
= 2 x + 4 |
| ( 2 3 ) x -
2 |
= 2 x + 4 |
| 2 3x - 6 |
= 2 x + 4 |
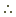 3x - 6 3x - 6 |
= x + 4 |
| 2x |
= 10 |
| x |
= 5 |
Other methods:
· Get the bases to be the same
· Factor out a common factor (involving an exponent)
| 3 x + 2 - 3
x |
= 216 |
|
| 3 x ( 3 2
- 1) |
= 216 |
|
| 3 x ( 9 - 1) |
= 216 |
find a common factor by
remembering your exponent laws (am an
= am+n ) and then follow BEDMAS rules. Then
find a common base and solve for x. |
| 3 x |
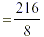 |
| 3 x |
= 27 |
| 3 x |
= 3 3 |
|
| x |
= 3 |
|
· Note knowing the powers of 2 from 0 to 10 is very helpful,
same with the powers of 3 from 1 to 5.
REMEMBER
· Reduce the expression to only two parts (one with an
unknown exponent and a constant term)
o Common methods  Factoring, BEDMAS
rules, Exponent laws Factoring, BEDMAS
rules, Exponent laws
· Find a common base
o NOTE zero can be an base with an exponent zero.
|