Imaginary Solutions to Equations
In the complex number system the even-root property can be restated so that x2
= k is equivalent to
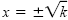 for any k
≠ 0. So an equation such as x2 =
-9 that has
no real solutions has two imaginary solutions in the complex numbers.
Example 1
Complex solutions to equations
Find the complex solutions to each equation.
a) x2 = -9
b) 3x2 + 2 = 0
Solution
a) First apply the even-root property:
| x2 |
= -9 |
|
| x |
= ± |
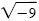Even-root property |
| |
= ± i |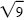
|
| |
= ± 3i |
|
Check these solutions in the original equation:
| (3i)2 |
= 9i2 = 9(-1) = -9 |
| (-3i)2 |
= 9i2 = -9 |
The solution set is {±3i}.
b) First solve the equation for x2:
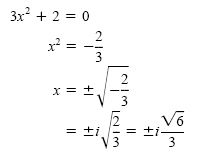
Check these solutions in the original equation. The solution set is
 .
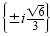The basic facts about complex numbers are listed below.
Complex Numbers
1. Definition of i:
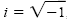 , and i2
= -1.
2. A complex number has the form a + bi, where a and b are real numbers.
3. The complex number a + 0i is the real number a.
4. If b is a positive real number, then
 .
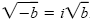5. The numbers a + bi and a - bi are called complex conjugates of each
other. Their product is the real number a2 + b2.
6. Add, subtract, and multiply complex numbers as if they were algebraic
expressions with i being the variable, and replace i2 by -1.
7. Divide complex numbers by multiplying the numerator and denominator
by the conjugate of the denominator.
8. In the complex number system x2 = k for any real number k is equivalent
to x = ±
 .
|
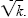