Multiplying Polynomials
Objective Learn the techniques of multiplying
two binomials by using the FOIL method, and multiplying
polynomials by using the Distributive Property.
In this lesson, you will use the technique of multiplying a
polynomial by a monomial, along with the Distributive Property,
to multiply any two polynomials.
Multiplying Binomials
Foil Method for Multiplying two Binomials
To multiply to binomials, find the sum of the products of
| F |
the First terms, |
| O |
the Outer terms, |
| I |
the Inner terms, and |
| L |
the Last terms. |
Example 1
Find (3x + 2)(2x + 4).
Solution
Apply the FOIL method by adding the product of the First,
Outer, Inner, and Last terms of the binomials.
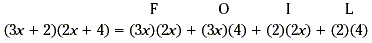
Now multiply and add like terms.
= 6x 2 + 12x + 4x + 8
= 6x 2 + 16x + 8
Example 2
Find (2x 2 - 1)(4x 3 - 3x ).
Solution
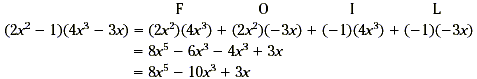
In multiplying more general polynomials, apply the
Distributive Property to write the product as a sum of products
of polynomials times monomials, and then use basic techniques to
multiply polynomials and monomials. Finally, simplify by adding
like terms.
While the following examples are relatively long and involve
several steps, you are already familiar with each of the
individual steps. If you work slowly and carefully, you will be
successful in solving these types of problems.
Example 3
Find (3x 2 + 2x +1)( x 3 - x ).
Solution
First use the Distributive Property to write this product as a
sum of products of polynomials times monomials.
(3x 2 + 2x +1)( x 3 - x ) = (3x 2
+ 2x +1)( x 3 ) + (3x 2 + 2x +1)( - x )
Then multiply each of the terms (again using the Distributive
Property).
= [(3x 2 )( x 3 ) + (2 x )( x 3
) + (1)( x 3 )] + [(3x 2 )(-x) + (2x )(-x)
+ (1)(-x)]
= 3x 5 + 2x 4 + x 3 - 3x
3 - 2x 2 - x
= 3x 5 + 2x 4 - 2x 3 - 2x
2 - x
Example 4
Find ( a 2 - 2a - 3)( a 2 - 4a - 3).
Solution
First use the Distributive Property to write this product as a
sum of products of polynomials times monomials.
( a 2 - 2a - 3)( a 2 - 4a - 3) = ( a
2 - 2a - 3)( a 2 ) + ( a 2 - 2a - 3)(-4a)
+ ( a 2 - 2a - 3)(-3)
Then use the Distributive Property to multiply each of the
terms.
= [( a 2 )( a 2 ) + ( - 2a )( a 2
) + ( -3)(a 2 )] + [( a 2 )( -4a ) + ( -2a
)( - 4a ) + ( -3)( -4a )] +
[( a 2 )( -3) + ( -2a )( -3) + ( - 3)( -3)]
= ( a 4 - 2a 3 - 3a 2 ) + ( -
4a 3 + 8a 2 + 12a ) + ( - 3a 2 +
6a + 9)
Now combine like terms to get the following.
= a 4 + ( -2a 3 - 4a 3 ) + (
- 3a 2 + 8a 2 - 3a 2 ) + (12a +
6a ) + 9 = a 4 - 6a 3 + 2a 2 +
18a + 9
|