|
TUTORIALS:
|
The Equation of a Circle
A circle is the set of all points equidistant from a single fixed point in a
plane. The single fixed point is called the center of the circle. The distance
from the center to any point on the circle is called the radius.
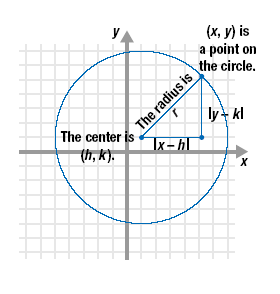 This circle is drawn on a Cartesian coordinate system.
In the figure:
• The ordered pair (h, k) is the center of the circle.
• The ordered pair (x, y) represents any point on the circle.
• The radius, r, is the distance between the center of the circle, (h, k),
and any point on the circle, (x, y).
| Now we may use the distance
formula to express the distance
between the center of the circle
and any point on the circle. That
distance is the radius of the circle. |
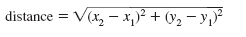 |
In the distance formula, make the following substitutions:
| distance = r
(x1, y1) = (h, k)
(x2, y2) = (x, y) |
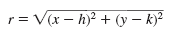 |
| To remove the square root,
square both sides. |
r2 = (x - h)2 + (y - k)2 |
The result is the equation of a circle.
This equation is usually written with r2 on the right.
Formula — The Equation of a Circle
The equation of a circle in the xy-plane is given by
(x - h)2 + (y - k)2 = r2
where the point (h, k) is the center of the circle, (x, y) is any point on
the circle, and r is the radius of the circle.
Example 1
Find the equation of the circle with center at (-4, 3) and radius 2.
| Solution
|
(x - h)2 + (y - k)2 = r2 |
| In the equation of a circle,
substitute -4 for h, 3 for k, and 2 for r.
Simplify. |
(x - (-4))2 + (y - 3)2 = 22
(x + 4)2 + (y - 3)2 = 4 |
The equation of the circle is (x + 4)2 + (y - 3)2 = 4.
Example 2
Find the center and the radius of the circle whose equation is
(x - 5)2 + (y + 3)2 = 16.
Solution
| The given equation has almost the same form as the standard equation of a circle.
x - 5 has the form x - h. Therefore, h is 5.
y + 3 does not have the form y - k. Rewrite y + 3 as y - (-3).
Therefore, k is -3.
r2 is 16.
Therefore, r is
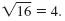 |
(x - h)2 + (y - k)2 = r2
(x - 5)2 + (y + 3)2 = 16
(x - 5)2 + (y - (-3))2 = 16 |
The center of the circle, (h, k), is (5, -3). The radius, r, is 4.Example 3
Find the center and the radius of the circle with equation
(x + 1)2 + y2 = 20.
Solution
| The given equation has almost the same form as the standard equation of a circle.
Rewrite x - 1 as x - (-1).
Rewrite y2 as (y - 0)2.
Now, we can identify h, k, and r. |
(x - h)2 + (y - k)2 = r2
(x + 1)2 + y2 = 20
[x - (-1)]2 + y2 = 20
[x - (-1)]2 + (y - 0)2 = 20
|
x - (-1) has the form x - h. Therefore, h is -1.
y - 0 has the form y - k. Therefore, k is 0.
r2 is 20. Therefore, r is
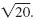
The center of the circle, (h, k), is (-1, 0). The radius is
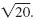
Note:
We can also write
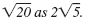
|