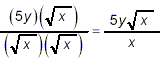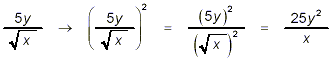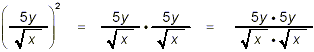Home |
Rationalizing the DenominatorThis document introduces an important method of algebraic simplification used when radicals involve fractions, or equivalently, when a fraction contains radicals in its denominator. Generally speaking, fractions with radicals in their denominators are considered to be less simple than equivalent fractions with no radicals in their denominator. The process of starting with a fraction containing a radical in its denominator and determining the simplest equivalent fraction with no radical in its denominator is called rationalizing the denominator. (This terminology arises from the fact that generally, radical expressions evaluate to give so-called irrational numbers , whose decimal part never terminates and never achieves a repeated pattern of digits. By eliminating the radical expression from the denominator, we are turning something which gives irrational number values to something which does not give irrational number values – hence the term “rationalizing” the denominator.) There is a general strategy for attempting to rationalize denominators containing radicals of any order. However, in this document, we will focus particularly only on fractions with square roots in the denominator. Whenever we attempt to manipulate a fraction to get a new fraction which is equivalent but simpler or easier to work with, it is important to ensure that we really do end up with an equivalent fraction. There are many ways to get rid of a square root. (We could simply square it, or we could even just erase it!). We must be careful to use a method which simultaneously makes the square root in the denominator disappear, but leaves us with a mathematically equivalent To start with one fraction and turn it into another equivalent fraction, we can simply multiply the numerator and denominator by the same thing. Secondly, to rationalize the denominator of a fraction, we could search for some expression that would eliminate all radicals when multiplied onto the denominator. Putting these two observations together, we have a strategy for turning a fraction that has radicals in its denominator into an equivalent fraction with no radicals in the denominator. (i) deduce a factor which can be multiplied onto the denominator to eliminate all radicals in it. (We will illustrate patterns of such factors for the most commonly occurring simple expressions containing square roots.) (ii) multiply both the numerator and the denominator of the fraction by this factor. (Then, the radicals will disappear from the denominator, and since we are multiplying the numerator and denominator by the same thing, the result will be a fraction which is equivalent to the original fraction.) (iii) carry out any necessary or feasible simplifications of the fraction coming out of step (ii). The tricky part here is step (i). It is easily possible to write down fractions with radicals in their denominators for which step (i) cannot be achieved. However, there are effective standard approaches for most situations commonly occurring in technical applications.
Example 1: Simplify solution: The square root,
since Remark: People sometimes mistakenly attempt to rationalize the denominator in a fraction such as the one we started with in Example 1 by simply squaring the fraction:
Now, it is true that this final form does have a rational denominator – the square root part has disappeared. However, this final from is in no way equivalent to the original fraction. You can easily see this by noting that
and so, squaring the original fraction amounts here to
multiplying the numerator by 5y and the denominator by
|
, in the denominator of
this fraction obviously cannot be simplified further. However, it
is in the denominator of this fraction, and so to simplify this
expression, we do need to rationalize the denominator. To achieve
this, we just need to multiply the numerator and denominator of
the fraction by the square root occurring in the denominator
(since this square root is already in simplest form). This gives
. The expression on the
right just above is a fraction in simplest form. It is equivalent
to the original fraction given at the beginning of this example
because all we did was multiply the numerator and denominator of
that original fraction by the same thing. Finally it has no
square root in the denominator. Hence it is the desired final
answer here. 
