|
TUTORIALS:
|
Exponents and Roots
Integer Exponents
Recall that 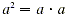 , while , while 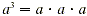 , and so on. In this section a more
general meaning is given to the symbol , and so on. In this section a more
general meaning is given to the symbol 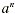 . .
DEFINITION OF EXPONENT
If n is a natural number, then
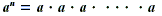
where a appears as a factor n times.
In the expression 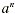 n is the exponent and a is the base. This
definition can be extended by defining n is the exponent and a is the base. This
definition can be extended by defining 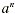 for zero
and negative integer values of n . for zero
and negative integer values of n .
ZERO AND NEGATIVE EXPONENTS
If a is any nonzero real number, and if n is a positive
integer, then
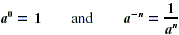
(The symbol 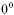 is meaningless.) is meaningless.)
EXAMPLE 1
Exponents
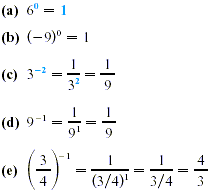
The following properties follow from the definitions of
exponents given above.
PROPERTIES OF EXPONENTS
For any integers m and n, and any real numbers a and b for
which thefollowing exist:
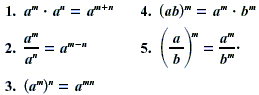
EXAMPLE 2
Simplifying Exponential Expressions
Use the properties of exponents to simplify each of the
following. Leave answers with positive exponents. Assume that all
variables represent positive real numbers.
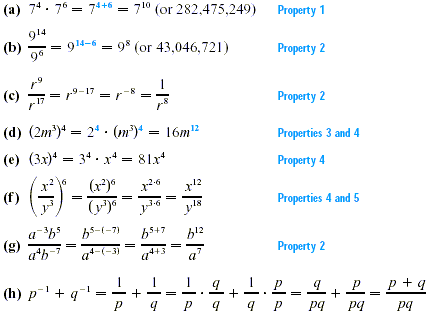
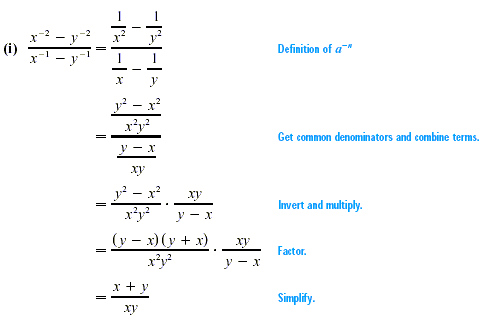
CAUTION
If Example 2(e) were written 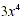 , the
properties of exponents would not apply. When no parentheses are
used, the exponent refers only tothe factor closest to it. Also
notice in Examples 2(c), 2(g), 2(h), and 2(i) that anegative
exponent does not indicate a negative number. , the
properties of exponents would not apply. When no parentheses are
used, the exponent refers only tothe factor closest to it. Also
notice in Examples 2(c), 2(g), 2(h), and 2(i) that anegative
exponent does not indicate a negative number.
|